Did you read Fortran77? Yes, you did. This is just a silly project I made, because I am curious about old languages. I want to tell you some facts I found out about this language using this example.
But first comes the project code and some explanations:
program
implicit none
double precision pi, res, integral, testfun1, testfun2, a, b
double precision recvdata
external testfun1, testfun2
integer n, pipetail
parameter (n=20)
integer makepipe, topid, id, np, links(2), nprocs
np = nprocs()
pipetail = np - 1
topid = makepipe(1, np, -1, -1, -1, -1, -1, -1, id, links)
pi=4.d0*datan(1.d0)
a = 0
b = pi
call sliceinterval(a, b, id, np)
res = integral(testfun1, a, b, n)
if(id.ne.0) then
call recv(topid, links(1), recvdata, 8)
print*, "id", id, ", recieved", recvdata
endif
res = res + recvdata
if(id.ne.pipetail) then
call send(topid, links(2), res, 8)
endif
if(id.eq.pipetail) then
print*,"testfunction 1"
print*,"integral", res
print*,"pi", pi
print*,"distance", abs(res-pi)
print*,""
endif
call freetop(topid)
end
C sets new interval boundaries based on the own id and number of processors
subroutine sliceinterval(a, b, id, np)
double precision a, b, h
integer id, np
h = (b-a) / np
a = a + id * h
b = a + h
end
C the first testfunction
double precision function testfun1(x)
double precision x
testfun1 = x * dsin(x)
end
C the second testfunction
double precision function testfun2(x)
double precision x
testfun2 = 4/(1 + x*x)
end
C calculates the integral of the given function fun in the interval [a,b]
C with n steps
double precision function integral(fun, a, b, n)
double precision fun, a, b, h, integral, xs
integer n, i, c
h = (b-a)/n
integral = fun(xs(0,a,h))
do i=1,n-1
c = 2 + 2 * mod(i,2)
integral = integral + c * fun(xs(i,a,h))
enddo
integral = (integral + fun(xs(n,a,h))) * h/3
end
C returns x_i for the given i (index), a (interval start) and h (with h=(b-a)/n)
double precision function xs(i,a,h)
integer i
double precision a,h
xs = a + i*h
end
This simple program will calculate the integral of any given function (in this case testfunction1) in any given interval by using the formula:
the interval is [a,b]
integral(f(x)) = h/3(y0 + 4*y1 + 2*y2 + 4*y3 + ... + 2*yn-2 + 4*yn-1 + yn)
h = (b-a)/n
The result is just an approximation, so for testing it I chose a testfunction whose integral will be PI in the interval [0, pi] and compared it to the machine PI I can calculate using atan.
The same can be done with testfunction2 in the interval [0,1], which will also result in PI.
To work with multiprocessors, the parex library is used. Every processor calculates the integral of a part of that interval given. I chose to build a pipe as virtual architecture and then populate and sum up the result from the first processor to the last.
I.e. processor with id 0 will calculate the integral 1,1
id 1 receives the result and adds it to it's own calculation, 1,1 + 0,2 = 1,3.
id 2 gets the result from id 1 which is 1,3 and so on until you get to the very end of the pipe where the final result will be printed.
Here is the output of the code above:
id 1, recieved 1.9876787099988892E-02
id 2, recieved 0.1517464117063354
id 3, recieved 0.4730412324368839
id 4, recieved 0.9999999975225691
id 5, recieved 1.675276693198365
id 6, recieved 2.373187882619952
id 7, recieved 2.922329941636222
testfunction 1
integral 3.141592656184073
pi 3.141592653589793
distance 2.5942803461020958E-09
Now some silly facts about fortran77: This old fortran version still has some remains from the times where you used punchcards to write your program.
Look at this punchcard for example:
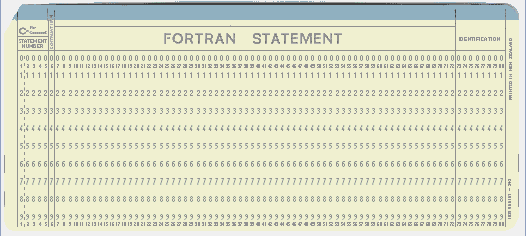
There you have several sections in the columns. In the first column there will be a C if a comment is following. Col 2-5 are for statement numbers (where you can jump to). Col 6 can be punched to mark a continuation from the last line.
Col 7-72 is actual source code (the section in the middle) and everything after that won't be read at all by fortran and can be used for anything you like (often used for identifying information).
Again: This punchcard was used for the very first version of Fortran which appeared in 1957. If you are interested in that, read more about it here:
http://www.fortran.com/FortranForTheIBM704.pdfFortran77 came 20 years later and still you had to adhere the structure of the punchcards. That means you can only write code from column 7 to 72, otherwise the compiler will complain. You also have to mark comments with a C in the very first column and so on. You can't get any commandline arguments.
However, I was surprised that I could just pass a function as an argument. That's something I didn't expect from an old language like that. I also feel that Fortran77 is still more comfortable to program with than C.
Fotran uses call-by-reference, so any parameter you change in a subroutine or function is changed within the caller too.
The functions are a bit weird. The result is always the value of the variable that has the same name as the function when either "end" or "return" statement is reached.
You also declare the types of the parameters in the first lines of the body.
Speaking of types: Fortran has implicit type declaration which probably came from the fact that the inventor Backus was a mathematician or had a firm mathematical background. Every variable or function whose name starts with i, j, k, l, m or n is an integer (note that these are common names for indices and the like in mathematical formulas), everything else will be a real (which is a single precision floating point number, or float in C).
I decided to explixitly declare every type nevertheless to avoid confusion.
Fortran77 is also case insensitive. Doesn't matter if you write Name, name, nAME, NAME, it will all be the same for the compiler.
That's it for now.
Have fun coding.
Deque