[TUTORIAL]Rendering fractals in a programming langauge

[Danus]

Oh Hi there, I'm Danus and I'm a programmer and a struggling malware analyst but not a mathematician, recently I stumbled upon something amazing:







No, this is not photoshop ladies and gentleman these are fractals.
So before we code one lets go a bit back to maths and boring sadness.

Complex Numbers and the Complex Plane
What is a Complex number?

Well before we go to that lets imagine a graph!

On our graph we got an axis which contains natural numbers -

(-2)-(-1)-0-1-2-3-4-5-6-7-8-9->(real)

We shall call it the real axis.

Now imagine we draw another Axis that goes up and down, in this magic land a number with a negative square root can exist and we shall call it the imaginery axis


5
|
4
|
3
|
2
|
1
|
0-1-2-3-4-5

This is called the Complex plane, where Real numbers and Imaginery numbers exist.

Say we want to use a point where the real number equals 3 and the imaginery number equals 2, we shall express them like so 3+2i. I wont get into calculating Complex numbers and proving the theory here because Im not a mathematician so this is all you need to know.(for now)

A Bounded point and a point escaping to infinity

before we code we will explore the fractal world together using this website -

http://szczypka.web.cern.ch/szczypka/home/julia.html this

this ladies and gentleman is a Julia set fractal renderer but the name is not important right now.
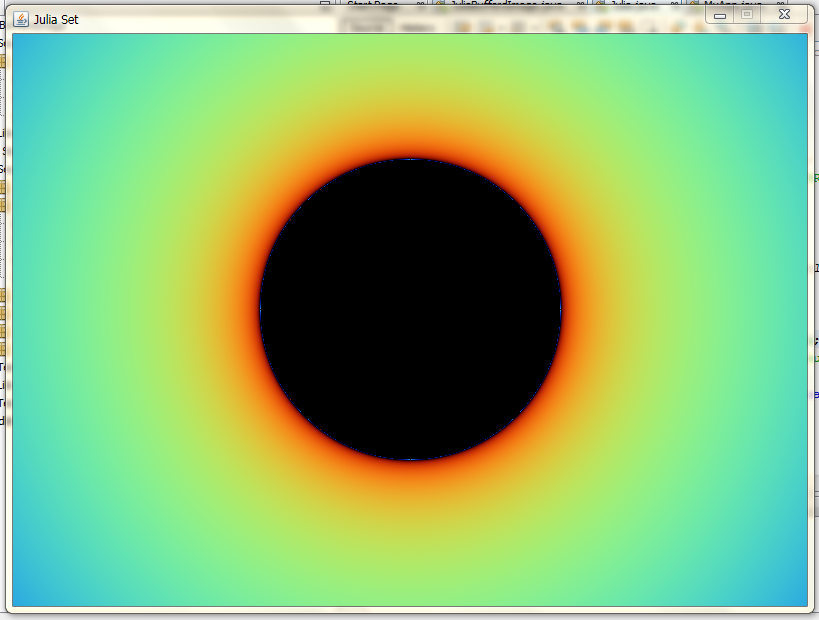
For settings please click boolean and set RE and IM to 0 it would look this -

Go ahead and click update, you should get a plane black and white circle.

Lets simulate a graph, with our screen size resolution while each pixel is a number!

now if we scan each pixel and apply the following function on it Z = Z^2
(While Z being a complex form of the pixel cordient, so say we want to represent the first pixel
Z would be equal to Complex(XPixelPos, YPixelPos), we shall loop under this formula 4 times, in other words the formula will go through 4 iterations.
The following can happen:
1. the point will loop inside itself until it would get stuck and move no futher.
2.the point will move a few positions and then get stuck
3. the point will escape to infinity.

How do we know the point escaped or not you ask? well according to math if the point left the radius 4 on the real axis then the point will probably escape to infinity! and how do we check if it left the 4 radius? well
we calculate the final absolute value of the point and check if its bigger than 4, we color it white else we color it black!

and thats where the math comes in!

say we want to calculate if the point Complex(1,4) escapes to infinity after 4 iterations well lets check.


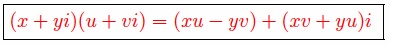
1st iteration: (1*1)-(4*4)+(1*4)i+(4*1)i = (1)-(16)+(4)i+(4)i= -15+8i = Complex(-15,8i)
2nd iteration: 161-240i
3rd iteration: -31679-77280i
4rd iteration: -4968639359+4896306240i(you can probably guess this point kinda ran away)

(I used http://www.mathsisfun.com/numbers/complex-number-calculator.html for 2nd-4th calculations)

so to check if that final point did actually ran off we grab the absolute value of the final result using the following formula SquareRoot(real*real + imaginery*imaginery) - this returns a natural real number and we check if its bigger than 4.

the point escaped to infinity can guess it probably, wont even bother calculating it.

So we shall color this pixel white!

but wait you say we dont have a code! We have that renderer i gave you before which would be great to check this out!

http://szczypka.web.cern.ch/szczypka/home/julia.html
so again set Real and Im to 0 and update and you should get a boring circle, keep in mind that this is a fractal!

The Julia Set

So before I showed you how the fractals work, But say I want to check if a point is bounded under the formula Z = Z^2 + C while Z being the pixel position and C being a constant Complex Number. What this formula does is each iteration moves the final Z result by C units, go a head and check what happens if we use Z = Z^2 + Real(0.5), What this does is moves the final Z result by 0.5 units ont the real axis each time. you are welcome to choose any color you want. because boolean wont show a proper result since this time we would color each point in the amount of time it takes it to escape! How much time it takes it to escape you ask?! well the amount of iterations it passes before it escapes to infinity! if how ever we looped it through 1000 iterations and it still didnt escape we can safley color it black knowing it will probably never escape!

for a more intresting result go a head and insert Real (0.5) and IM(0.2).


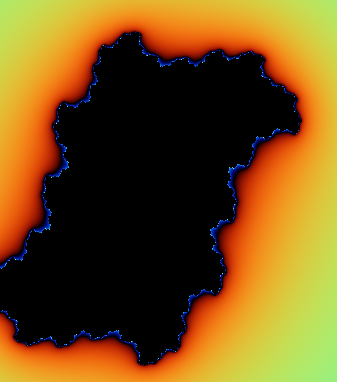
A julia set renderd in my own java renderer!

These fractals are called the Julia sets!

The MandelBrot Set
So before we disscussed julia sets, Notice how we have black pits in some julia sets, and some that dont have black pits at all! This means if the julia contains atleast one black pit its bounded how ever if it contains 0 pits its not bounded which means the whole set will escape to infinity!



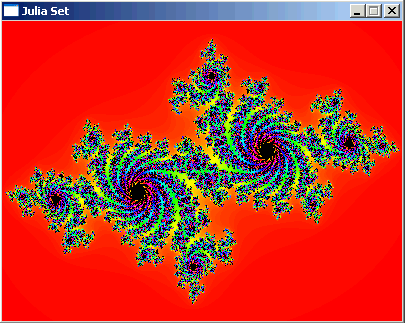
(Bounded Julia sets)


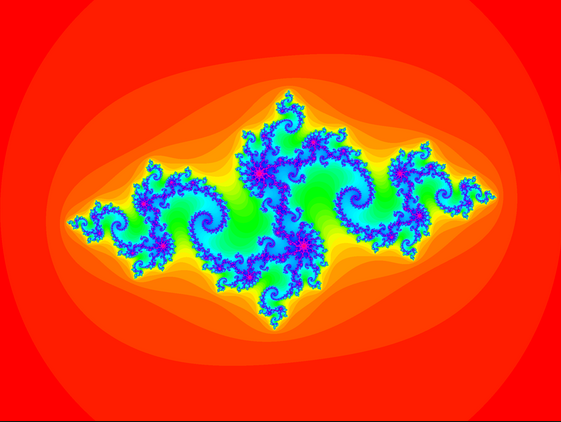
(A julia set which escaped to infinity)

But the more intresting find is that if the Point Complex(0,0) which is the center of the screen or the point (0,0) is bounded the set would contain an amount of black pits , how ever if Complex(0,0) escapes to infinity then no black pits would exist on the graph.  Now no matter what C you would give me, by calculating Z(0,0i)= Z^2 + C I would know if the julia set is bounded or not!
Now what if i would make a fractal while looping through the julia sets located on my screen while we know a julia set is bounded if its Complex(0,0) doenst escape to infinity under Z = Z^2 + C.  While C being a pixel cordient each time. so say looping through the first pixel would be Z(0,0) = Z^2 +C(XPixelPos,YPixelPos). we color each pixel by the amount of time it takes it to escape to infinity.
So lets loop through each pixel cordinet corresponding to the point Complex(0,0) by 1000 iteartions.







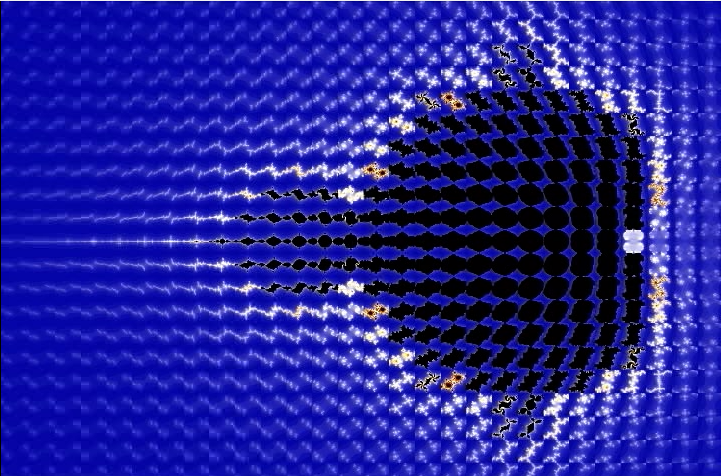
We got the mandelbrot set which is constructed out of the sum of julia sets corresponding to point Complex(0,0)

CODING TIME!!!!!!!!
The code would be written in java, HOW EVER you are welcome to port it to what ever langauge you want. ill try keeping it simple incase you dont know java!

Coding a Julia Set
First of all lets set up a bufferd Image object, this class in java allows us to create a window in desirable resolution and color its pixels!

So lets open up a class file

Code: [Select]

import java.awt.Graphics;
import java.awt.image.BufferedImage;
import javax.swing.JFrame;
 
public class Julia extends JFrame {
 
    private final int MAX_ITER = 1000; // MAX iterations
    private final double ZOOM = 150; // Zoom..
    private BufferedImage I;
    private Complex c,z;
 
    public Julia() {
        super("Julia Set");
        setBounds(100, 100, 800, 600); // Resolution set up - 800x600.
        setResizable(false);
        setDefaultCloseOperation(EXIT_ON_CLOSE);
        I = new BufferedImage(getWidth(), getHeight(), BufferedImage.TYPE_INT_RGB);
     }
}

Keep in mind that I'm using a custom Complex number class which can be found online
http://introcs.cs.princeton.edu/java/97data/Complex.java.html

Ok so we got our basics now, we need to loop through the x cordients and the y cordients through 1000 iterations, this could be done with 2 for loops and 1 while loop or 3 for loops, ill show you both ways!

So lets remember that the constant in the Julia set is the C value of the formula and the changing variable is the Z value of the formula which represents each pixel on the screen.

Code: [Select]

c = new Complex(0,0); // Setting up a new C constant with the points 0,0
for (int y = 0; y < getHeight(); y++) {
            for (int x = 0; x < getWidth(); x++) {
                z = new Complex((x - getWidth()/2) / ZOOM,(y - getHeight()/2) / ZOOM) // Looping through        the cordients, keep in mind that x and y can go below 0 so the 0,0 point has to be in the middle of the screen.
            }
      }
}


And now for the complex part, we are going to check if the point is bounded or not.

Code: [Select]

c = new Complex(0,0); // Setting up a new C constant with the points 0,0
        for (int y = 0; y < getHeight(); y++)
        {
            for (int x = 0; x < getWidth(); x++)
            {
                int iter = 0; // Looping through iterations
                z = new Complex((x - getWidth()/2) / ZOOM,(y - getHeight()/2) / ZOOM);
                while (z.abs() < 4 && iter < MAX_ITER) // If the absolute value of Z ESCAPED or the iterations are bigger than the maximum defined, then exit loop
                {
                    z = z.times(z).plus(c);//Z = Z^2 + C
                    iter++;
                }
               
                if(iter < MAX_ITER) // The while loop was terminated because z.abs() < 4 so color the point in the time it took it to escape! (im using a special formula where i color by escape-time*z.absolute())
                    I.setRGB(x, y, (int)(iter*z.abs()));
                else
                    I.setRGB(x, y, 0); // the while loop was terminated because the iterantions have reached max so of this point is color black.
            }
        }
    @Override
    public void paint(Graphics g) { //drawing function
        g.drawImage(I, 0, 0, this);
    }
 
    public static void main(String[] args) { //executing main in class file!
        new Julia().setVisible(true);
    }
}

Final code should look like this -

Code: [Select]

import java.awt.Graphics;
import java.awt.image.BufferedImage;
import javax.swing.JFrame;
 
public class Julia extends JFrame {
 
    private final int MAX_ITER = 1000;
    private final double ZOOM = 150;
    private BufferedImage I;
    private Complex c,z;
 
    public Julia() {
        super("Julia Set");
        setBounds(100, 100, 800, 600);
        setResizable(false);
        setDefaultCloseOperation(EXIT_ON_CLOSE);
        I = new BufferedImage(getWidth(), getHeight(), BufferedImage.TYPE_INT_RGB);
        c = new Complex(0,0); // Setting up a new C constant with the points 0,0
        for (int y = 0; y < getHeight(); y++)
        {
            for (int x = 0; x < getWidth(); x++)
            {
                int iter = 0;
                z = new Complex((x - getWidth()/2) / ZOOM,(y - getHeight()/2) / ZOOM);
                while (z.abs() < 4 && iter < MAX_ITER) {
                    z = z.times(z).plus(c);
                    iter++;
                }
               
                if(iter < MAX_ITER)
                    I.setRGB(x, y, (int)(iter*z.abs()));
                else
                    I.setRGB(x, y, 0);
            }
        }
    }
   
    @Override
    public void paint(Graphics g) {
        g.drawImage(I, 0, 0, this);
    }
 
    public static void main(String[] args) {
        new Julia().setVisible(true);
    }
}
This is the while variation which I prefer to use how ever here is the for loop variation.

Code: [Select]

                for(int i = 0; i <= MAX_ITER ; i++) {
                    z = z.times(z).plus(c);
                    iter++;
                    if(z.abs() > 4)
                    {
                        I.setRGB(x, y, (int)(iter*z.abs()));
                        break;
                    }
                }
                     if(iter >= MAX_ITER)
                        I.setRGB(x, y, 0);


You are welcome to change C and run the program again and again, keep in mind that the more iterations you do for each point, its color will be more correct - how ever we are missing a few things here:

1.SMOOTHING, you see those ugly blue layers? they shouldnt exist the colors should smooth out through the entire set.
2.A nicer coloring algorithm
3.Proper Zooming, it just zooms to the center if we change the zoom.

Lets add a smoothing algorith which works on the following formula -
Smooth = Math.cbrt((double)(iter)+1-log(log(z.abs(),2),2))*(0.5); which means

Cuberoot(Iterations+1-log2(log2(z.abs()))*(0.5)) while 0.5 being a smoothing scale, you can change it how ever i have no clue how it works and what it does since im not a mathematican im just trying to port math to java. I used the following custom function to get base (2) log.

Code: [Select]

    static double log(double x, int base)
    {
        return (double) (Math.log(x) / Math.log(base));
    }

so lets add a new variable, double smooth;

and instead of using iterations to color it we used the smoothed value to color it.
now we shall add a proper coloring algorithm which colors it by the time it takes it to escape how ever, this time it will depend on a new coloring table. more time to escape will cause the point to be more bright and if it takes it a short time to escape we will color it dark blue. so the coloring table which corresponds to this coloring is rbg type and it runs between 0 and 1.
so what we do is we take the fractional part out of the smoothing value.
smooth = (smooth - Math.floor(smooth));

*

Now we create 3 new values which will work as the R G B values, these are double type values;

double colr = 9*(1-smooth)*smooth*smooth*smooth;
double colg = 15*(1-smooth)*(1-smooth)*smooth*smooth;
double colb = 8.5*(1-smooth)*(1-smooth)*(1-smooth)*smooth;

This would return a number between 0 to 1.

So lets code this bich:

Code: [Select]

c = new Complex(0,0); // Setting up a new C constant with the points 0,0
        for (int y = 0; y < getHeight(); y++)
        {
            for (int x = 0; x < getWidth(); x++)
            {
                int iter = 0;
                z = new Complex((x - getWidth()/2) / ZOOM,(y - getHeight()/2) / ZOOM);
                while (z.abs() < 4 && iter < MAX_ITER) {
                    z = z.times(z).plus(c);
                    iter++;
                }
               
                mu = Math.cbrt((double)(iter)+1-log(log(z.abs(),2),2))*(0.5); // mu being the smoothing variable.
                mu = (mu - Math.floor(mu)); // stealing the fractional part out of mu.
                   
                double colr = 9*(1-mu)*mu*mu*mu;
                double colg = 15*(1-mu)*(1-mu)*mu*mu;
                double colb = 8.5*(1-mu)*(1-mu)*(1-mu)*mu;
               
                Color c = new Color((float)colr,(float)colg,(float)colb); // we create a new RGB color using a class java provides.
               
                if(iter < MAX_ITER)
                    I.setRGB(x, y, c.getRGB); // since setRGB can only recieve a full RGB interger we have to apply a function on c to get the integer type of color c.
                else
                    I.setRGB(x, y, 0);
            }
        }

So the final code should look something like this:

Code: [Select]

package juliabufferdimage;

/**
 *
 * @author Danus
 */
import java.awt.Color;
import java.awt.Graphics;
import java.awt.image.BufferedImage;
import javax.swing.JFrame;
 
public class Julia extends JFrame {
 
    private final int MAX_ITER = 570;
    private final double ZOOM = 150;
    private BufferedImage I;
    private Complex c,z;
    private double mu;
 
    public Julia() {
        super("Julia Set");
        setBounds(100, 100, 800, 600);
        setResizable(false);
        setDefaultCloseOperation(EXIT_ON_CLOSE);
        I = new BufferedImage(getWidth(), getHeight(), BufferedImage.TYPE_INT_RGB);
        c = new Complex(0.25,0.5); // Setting up a new C constant with the points 0,0
        for (int y = 0; y < getHeight(); y++)
        {
            for (int x = 0; x < getWidth(); x++)
            {
                int iter = 0;
                z = new Complex((x - getWidth()/2) / ZOOM,(y - getHeight()/2) / ZOOM);
                while (z.abs() < 4 && iter < MAX_ITER) {
                    z = z.times(z).plus(c);
                    iter++;
                }
               
                mu = Math.cbrt((double)(iter)+1-log(log(z.abs(),2),2))*(0.5);
                mu = (mu - Math.floor(mu));
                   
                double colr = 9*(1-mu)*mu*mu*mu;
                double colg = 15*(1-mu)*(1-mu)*mu*mu;
                double colb = 8.5*(1-mu)*(1-mu)*(1-mu)*mu;
               
                Color c = new Color((float)colr,(float)colg,(float)colb);
               
                if(iter < MAX_ITER)
                    I.setRGB(x, y, c.getRGB());
                else
                    I.setRGB(x, y, 0);
            }
        }
    }
   
    static double log(double x, int base)
    {
        return (double) (Math.log(x) / Math.log(base));
    }
   
    @Override
    public void paint(Graphics g) {
        g.drawImage(I, 0, 0, this);
    }
 
    public static void main(String[] args) {
        new Julia().setVisible(true);
    }
}

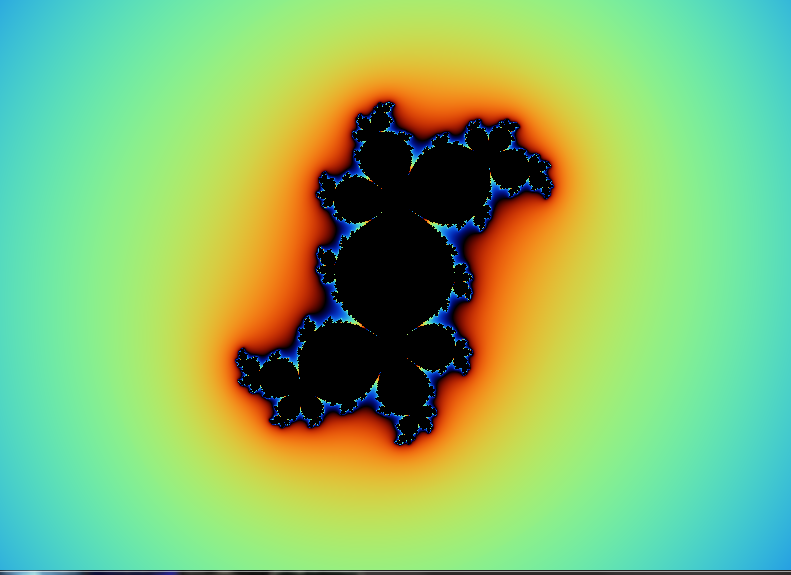
Go a head and run the code and you should get something like this:



but this shape is created under C = new Complex(0,0), lets try C = new Complex(0.25,0.5):



CHALLANGE

Alright ill leave some stuff for you to make so I wont spoon feed your lazy asses.

1. Add proper zooming, this means you can zoom in any point of the fractal, this is very intresting because the fractal is infinite so you can constatly find new shapes.

2.create a renderer for the mandelbrot set, keep in mind that in a mandelbrot set the Z is a constat (0,0) and the C is changing and it depends on the pixels in the frame, so C = Complex(XPixelPox,YPixelPos)

3.Add a loading bar in the console output or in the GUI and make it show how much time is remaining before the fractal finishes rendering.

Intresting websites and videos
https://www.youtube.com/watch?v=NGMRB4O922I - How the mandelbrot set works from the words of a mathematician.
https://www.youtube.com/watch?v=0jGaio87u3A - Zooming inside a mandelbrot set

fractalforums.com - Fell in love with fractals??! this is the place for you, filled with a bunch of nerds who create really amazing things. if you have any questions about more math you are welcome to ask there, its a very amazing community.

Well thats it ladies and gents, I hope this tutorial was good enough and you learned something new!!

[Stackprotector]

Great job! will read later.

[Deque]

Good writeup, Danus. You put some decent work into this article! +1

[Danus]

Good writeup, Danus. You put some decent work into this article! +1

Thanks ! it means a lot when its coming from you.